機械学習のエッセンス: 主要モデルの解説

機械学習とは

機械学習（Machine Learning）とは、大量のデータを読み込ませることで、データに内在しているパターンを学習させる結果、未知のデータを判断するためのルールを獲得することができるデータ解析技術です。

機械学習は「教師あり学習」「教師なし学習」「強化学習」の3つのカテゴリに分けられます。教師あり学習は、ラベル付きのデータを使ってモデルを学習し、新たな未見のデータに対する予測を行う手法です。一方、教師なし学習は、ラベルのないデータから構造やパターンを見つけ出すことに焦点を当てています。

機械学習の主要な手法とモデルを紹介します。具体的には、回帰や分類といった予測タスクから、クラスタリングや主成分分析といったデータ構造の探索まで、今回は10種類を紹介します。

教師学習あり / なし	種類	モデル
教師学習あり	回帰	線形回帰
	分類	サポートベクターマシン
		決定木
		アンサンブル学習（ランダムフォレスト）
		ロジスティック回帰
		ニューラルネットワーク
		ナイーブベイズ
教師学習なし	クラスタリング	k-means
		knn
	主成分分析	主成分分析（PCA）

下記のコードは、GoogleColaboratoryで確認をすることができます。ご自身のGoogleアカウントでも再現して手元で確認することができます。

今回のデータはsklearnライブラリのデータを利用しています。具体的には「カリフォルニアの住宅データセット」「アイリスデータセット」（アイリスとは、アヤメのことを指しています）。

なお、「アイリスデータセット」はデータサイエンスの世界でもっとも有名なデータセットの一つで、統計学の権威ロナルド・エイルマー・フィッシャーが論文で利用したデータセットです。

1. 線形回帰

モデルの概要

線形回帰は、2つ以上の変数間の関係をモデル化するための統計的手法です。特に、1つの従属変数（目的変数）と1つ以上の独立変数（説明変数）との間の線形相関関係を調査します。

利用パターン

線形回帰は、連続値の予測に適しています。たとえば、家の価格予測、売上予測、気温予測などです。

メリット

• 解釈が容易で、モデルの結果をビジネスの意思決定に直接使用することができます。
• 実装が簡単で、計算負荷が低い。

デメリット

• 線形性、独立性、等分散性、正規性といった厳格な前提条件が必要です。
• 外れ値に敏感で、データの分布がモデルの正確性に大きな影響を与えます。

サンプルコードと結果

Pythonのsklearnライブラリを使って線形回帰モデルを訓練し、評価するサンプルコードを示します。今回は、カリフォルニアの住宅データセットを使用します。

# カリフォルニアの住宅データセットの読み込み
from sklearn.datasets import fetch_california_housing
housing = fetch_california_housing()

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.datasets import fetch_california_housing
from sklearn.metrics import mean_squared_error

# データの読み込み
housing = fetch_california_housing()
X = housing.data
y = housing.target

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# モデルの訓練
model = LinearRegression()
model.fit(X_train, y_train)

# 予測の作成
y_pred = model.predict(X_test)

# モデルの評価
mse = mean_squared_error(y_test, y_pred)
print(f'平均二乗誤差: {mse}')

結果：平均二乗誤差: 0.5558915986952422

線形回帰モデルを訓練し、テストデータで評価します。評価指標として、平均二乗誤差(MSE)を使用します。MSEは、予測値と実際の値との差の二乗の平均を計算します。MSEが小さいほど、モデルの予測精度が高いと言えます。

2. サポートベクターマシン (SVM)

モデルの概要

サポートベクターマシン (SVM) は、分類や回帰分析に使用される教師あり学習モデルです。SVMは、データを高次元空間にマッピングし、超平面を見つけることでクラスを分離します。SVMの目標は、この超平面と最も近いトレーニングサンプルとの間のマージン（距離）を最大化することです。

利用パターン

SVMは、2クラス分類問題や多クラス分類問題、そして回帰問題に適用可能です。また、非線形問題に対してもカーネルトリックを用いることで対処可能です。

メリット

• 高次元データに対しても良好な性能を発揮します。
• カーネルトリックを用いることで非線形問題に対応可能です。

デメリット

• パラメータの選択とカーネルの選択が難しく、それにより性能が大きく左右されます。
• 大規模なデータセットでは、計算負荷が高くなる可能性があります。

サンプルコードと結果

Pythonのsklearnライブラリを使ってSVMを訓練し、評価するサンプルコードを示します。今回は、アイリスデータセットを使用します。

from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# データの読み込み
iris = load_iris()
X = iris.data
y = iris.target

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# モデルの訓練
model = SVC(kernel='linear')
model.fit(X_train, y_train)

# 予測の作成
y_pred = model.predict(X_test)

# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
print(f'正確度: {accuracy}')

結果：正確度: 1.0

このコードは、SVMを訓練し、テストデータで評価します。評価指標として、正確度（Accuracy）を使用します。正確度は、正しく分類されたサンプルの割合を表します。正確度が高いほど、モデルの予測精度が高いと言えます。

3. 決定木

モデルの概要

決定木は、データを分類または回帰するためのシンプルな学習アルゴリズムです。決定木の各ノードでは、特定の属性に基づいてデータが分割されます。これを再帰的に繰り返すことで、データをより細かく分割し、特定のクラスまたは値に到達します。

利用パターン

決定木は、分類問題と回帰問題の両方に使用できます。特に、特徴間の複雑な関係を探求する場合や、モデルの予測結果を解釈する必要がある場合に適しています。

メリット

• 結果の解釈が容易で、ビジネスルールとして利用可能です。
• データの前処理（例えば、特徴量のスケーリング）が必要ない。

デメリット

• 過学習（overfitting）しやすい。つまり、訓練データに対して高精度なモデルを作成するが、新しいデータに対してはうまく汎化できない。
• 線形性のあるデータに対しては、線形モデルに比べて性能が劣る場合がある。

サンプルコードと結果

Pythonのsklearnライブラリを使って決定木を訓練し、評価するサンプルコードを示します。今回は、アイリスデータセットを使用します。

from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# データの読み込み
iris = load_iris()
X = iris.data
y = iris.target

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# モデルの訓練
model = DecisionTreeClassifier()
model.fit(X_train, y_train)

# 予測の作成
y_pred = model.predict(X_test)

# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
print(f'正確度: {accuracy}')

結果：正確度: 1.0

このコードは、決定木を訓練し、テストデータで評価します。評価指標として、正確度（Accuracy）を使用します。正確度が高いほど、モデルの予測精度が高いと言えます。

4. アンサンブル学習（ランダムフォレスト）

モデルの概要

アンサンブル学習は、複数の学習アルゴリズムを組み合わせて作動させる手法です。ランダムフォレストはアンサンブル学習の一種で、多数の決定木を訓練し、それらの結果を平均化（回帰の場合）または多数決（分類の場合）により最終的な予測を行います。

利用パターン

ランダムフォレストは分類問題と回帰問題の両方に使用できます。特に、特徴量が多く、データが複雑な場合や、過学習を防ぎたい場合に適しています。

メリット

• 決定木の過学習を防ぐことができます。
• 特徴量のスケーリングが不要で、特徴量の重要度を評価できます。
• 並列処理が可能で、大規模なデータセットに対しても高速です。

デメリット

• モデルの解釈性が低い（個々の決定木よりも解釈性が低い）。
• ハイパーパラメータのチューニングが必要です。

サンプルコードと結果

Pythonのsklearnライブラリを使ってランダムフォレストを訓練し、評価するサンプルコードを示します。今回は、アイリスデータセットを使用します。

from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# データの読み込み
iris = load_iris()
X = iris.data
y = iris.target

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# モデルの訓練
model = RandomForestClassifier(n_estimators=100, random_state=0)
model.fit(X_train, y_train)

# 予測の作成
y_pred = model.predict(X_test)

# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
print(f'正確度: {accuracy}')

結果：正確度: 1.0

このコードは、ランダムフォレストを訓練し、テストデータで評価します。評価指標として、正確度（Accuracy）を使用します。正確度が高いほど、モデルの予測精度が高いと言えます。

5. ロジスティック回帰

モデルの概要

ロジスティック回帰は、線形回帰と同様に、説明変数から目的変数を予測するためのモデルです。ただし、ロジスティック回帰は、目的変数がカテゴリカル（例えば、はい/いいえ、成功/失敗など）である場合に使用されます。

利用パターン

ロジスティック回帰は、二項分類問題に特に適しています。例えば、メールがスパムかどうかを分類したり、顧客が商品を購入するかどうかを予測したりする場合などです。

メリット

• モデルの出力を確率として解釈することができます。
• 説明変数と目的変数との関係を容易に理解することができます。

デメリット

• 線形分離可能な問題にしか適用できない。
• 外れ値や多重共線性（説明変数間の相関）の影響を受けやすい。

サンプルコードと結果

Pythonのsklearnライブラリを使ってロジスティック回帰モデルを訓練し、評価するサンプルコードを示します。今回は、アイリスデータセットを使用します。

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# データの読み込み
iris = load_iris()
X = iris.data
y = iris.target

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# モデルの訓練
model = LogisticRegression()
model.fit(X_train, y_train)

# 予測の作成
y_pred = model.predict(X_test)

# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
print(f'正確度: {accuracy}')

結果：正確度: 1.0

6. ニューラルネットワーク

モデルの概要

ニューラルネットワークは、脳のニューロンの動作を模倣したモデルで、深層学習の基礎となるものです。多数のニューロンが互いに連結され、信号（データ）を伝達しながら学習します。

利用パターン

ニューラルネットワークは、画像認識、自然言語処理、音声認識といった複雑な問題に対して優れた性能を発揮します。

メリット

• 大量のデータと複雑なパターンを学習する能力があります。
• テキスト、画像、音声など、さまざまなタイプのデータに対応可能です。

デメリット

• 学習には大量のデータと計算資源が必要です。
• モデルの内部構造が「ブラックボックス」であり、解釈が難しい場合があります。

サンプルコードと結果

以下に、Pythonのsklearnライブラリを使ってニューラルネットワーク（具体的には、多層パーセプトロン）を訓練し、評価するサンプルコードを示します。今回は、アイリスデータセットを使用します。

from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# データの読み込み
iris = load_iris()
X = iris.data
y = iris.target

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# モデルの訓練
model = MLPClassifier(hidden_layer_sizes=(10,), max_iter=1000)
model.fit(X_train, y_train)

# 予測の作成
y_pred = model.predict(X_test)

# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
print(f'正確度: {accuracy}')

結果：正確度: 1.0

7. ナイーブベイズ

モデルの概要

ナイーブベイズは、ベイズの定理に基づく確率的な分類アルゴリズムで、特徴間の独立性を仮定します（これが「ナイーブ（単純）」の由来です）。

利用パターン

ナイーブベイズは、テキスト分類（例えば、スパムメールのフィルタリングや感情分析）や推薦システムなどによく用いられます。

メリット

• 計算が高速で、大量のデータに対しても効率的に動作します。
• モデルの学習と予測が簡単です。

デメリット

• 特徴間の相互依存性を扱うことができません（これが「ナイーブ」の仮定です）。

サンプルコードと結果

Pythonのsklearnライブラリを使ってナイーブベイズ（具体的には、ガウシアンナイーブベイズ）を訓練し、評価するサンプルコードを示します。今回は、アイリスデータセットを使用します。

from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# データの読み込み
iris = load_iris()
X = iris.data
y = iris.target

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# モデルの訓練
model = GaussianNB()
model.fit(X_train, y_train)

# 予測の作成
y_pred = model.predict(X_test)

# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
print(f'正確度: {accuracy}')

結果：正確度: 1.0

8. k-means

モデルの概要

k-meansは、データをk個のクラスタに分けるためのアルゴリズムで、教師なし学習の一種です。k-meansは、各クラスタの重心（平均）を計算し、各データポイントを最も近い重心に基づいてクラスタに割り当てます。このプロセスを重心が変化しなくなるまで繰り返します。

利用パターン

k-meansは、市場セグメンテーション、画像分割、アノマリ検出など、データのクラスタリングが必要な場合に使用されます。

メリット

• アルゴリズムが単純で理解しやすい。
• 大量のデータに対しても比較的高速に動作します。

デメリット

• クラスタ数kを事前に設定する必要があります。
• 初期値の選択によっては、局所最適解に陥る可能性があります。

サンプルコードと結果

Pythonのsklearnライブラリを使ってk-meansを訓練し、クラスタリング結果を表示するサンプルコードを示します。今回は、アイリスデータセットを使用します。

from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

# データの読み込み
iris = load_iris()
X = iris.data

# モデルの訓練
model = KMeans(n_clusters=3)
model.fit(X)

# クラスタの予測
clusters = model.predict(X)

# 結果のプロット
plt.scatter(X[:, 0], X[:, 1], c=clusters)
plt.show()

このコードは、k-meansを訓練し、全てのデータに対してクラスタを予測します。その後、2つの特徴量を軸にしてデータをプロットし、色を使って各データポイントのクラスタを表示します。

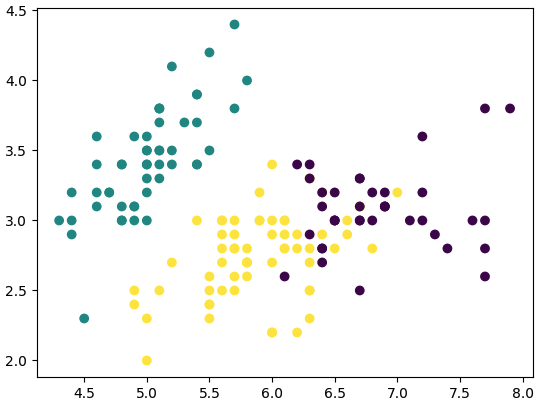
9. k-nearest neighbors (knn)

モデルの概要

k-nearest neighbors (knn) は、教師あり学習と教師なし学習の両方で使用されるアルゴリズムです。knnは、新しいデータポイントに対する予測を行うとき、訓練データセットの中で最も近いk個のデータポイント（「近傍」）を見つけ、これらの「近傍」のラベルや値から予測を行います。

利用パターン

knnは、分類問題と回帰問題の両方で使用できます。また、教師なし学習として、データのクラスタリングにも使用できます。

メリット

• アルゴリズムが単純で理解しやすい。
• 訓練データセットに対する学習が不要（怠惰学習）。

デメリット

• データセットが大きい場合、予測に時間がかかる。
• 特徴量のスケーリングが必要。

サンプルコードと結果

Pythonのsklearnライブラリを使ってknnを訓練し、評価するサンプルコードを示します。今回は、アイリスデータセットを使用します。

from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# データの読み込み
iris = load_iris()
X = iris.data
y = iris.target

# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# モデルの訓練
model = KNeighborsClassifier(n_neighbors=3)
model.fit(X_train, y_train)

# 予測の作成
y_pred = model.predict(X_test)

# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
print(f'正解率: {accuracy}')

結果：正解率: 1.0

このコードは、knnを訓練し、テストデータで評価します。評価指標として、正確度（Accuracy）を使用します。正確度が高いほど、モデルの予測精度が高いと言えます。

10. 主成分分析 (PCA)

モデルの概要

主成分分析（PCA）は、データの次元削減を行うための手法です。PCAは、データの分散が最大となる方向（主成分）を見つけ、その方向にデータを射影することで次元削減を行います。

利用パターン

PCAは、高次元データの視覚化、データのノイズ除去、特徴抽出、データの前処理などに使用されます。

メリット

• 高次元のデータを低次元に削減でき、データの可視化が容易になります。
• データのノイズを除去するのに有用です。

デメリット

• 主成分が元の特徴とは異なる新しい特徴を作るため、解釈が困難な場合があります。

サンプルコードと結果

Pythonのsklearnライブラリを使ってPCAを適用し、結果を表示するサンプルコードを示します。今回は、アイリスデータセットを使用します。

from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

# データの読み込み
iris = load_iris()
X = iris.data

# PCAの適用
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

# 結果のプロット
plt.scatter(X_pca[:, 0], X_pca[:, 1])
plt.xlabel('First Principal Component')
plt.ylabel('Second Principal Component')
plt.show()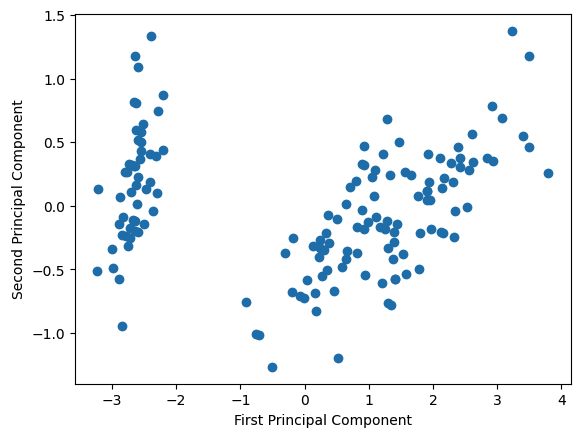

このコードは、PCAを適用して2次元にデータを削減し、その結果をプロットします。このように、PCAは高次元のデータを低次元に削減し、データの構造を可視化するのに役立ちます。